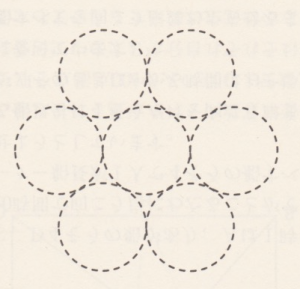
[解説] これは算数オリンピックの問題です。
回転して重なるものは同じと見なす事から、真ん中の位置はその周りの位置とは区別して考えが必要がありそうです。話題となっている黒い石は何個使っても良いので、黒い石を置く数で場合分けしましょう。
(ⅰ)黒い石が0個の場合
全部が白い石となるとき「黒い石同士が隣り合わない」という条件を満たしていますので、まず1通り。
(ⅱ)黒い石が1個の場合
真ん中に置くか周りに置くかですが、周りに1個置いたときは回転しても同じですね。ですからこの場合は2通りです。

(ⅲ)黒い石が2個の場合
黒を真ん中に置くと2個目と必ず接してしまうので周りに2個置くしかありません。

図のようになりますのでこの場合は2通りです。
(ⅳ)黒い石が3個の場合
これは次の1通りの場合しかありません
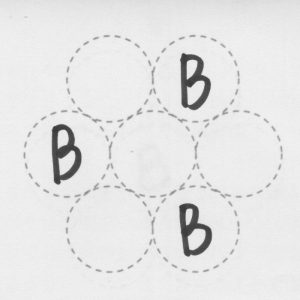
以上(ⅰ)〜(ⅳ)から
1+2+2+1=6 6通りです。
