「無限等比級数の和」が最もスッキリするのでは
循環小数から整数の比（分数）に直すもう一つの方法は
循環小数を「無限級数の和」としてとらえ計算するというものです。
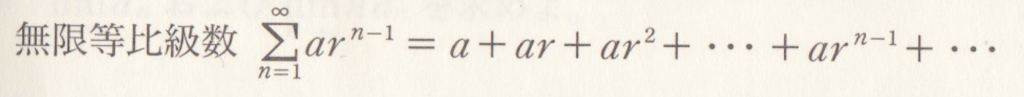
高校数学の数IIIの範囲になりますが、これは | r | ＜1 の時に収束してその和は
a/ (1-r)
となることが知られています。（まあともかくそうだと思ってください）
この公式を前提にすれば、 前回（7/ 循環小数 2) の
すなわち 0.333333・・・・は次の様にして整数の比に直せます。
0.3333333・・・・＝0.3 + 0.03 + 0.003 + 0.0003 +・・・・
は、初項が a = 0.3 で 公比 r = 0.1 の無限等比級数の和と考えられますので、上の公式を使えば
0.3333333・・・ = 0.3/ (1-0.1) = 0.3/0.9 = 1/3 （3分の1）とそのまま素直に出すことができます。
自分には前回の方法よりスッキリとしているのですが、若干知識が必要となりますね。
前回と今回と「同じ循環小数を分数に直す」という話でした。これはどちらが好みかというだけではなく、自分の数学の世界の広がりにともなって捉え方が変化して行くというダイナミズムが数学の醍醐味であることをぜひ知っていただきたいと思って取り上げました。